| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- DP
- Union-Find
- MST
- mergesorttree
- Tree
- Sweeping
- Dijkstra
- Implementation
- FenwickTree
- scc
- ShortestPath
- DFS
- KMP
- Bellman-Ford
- IndexedTree
- topologicalsort
- Floyd
- greedy
- 2-sat
- TwoPointers
- backtracking
- Bridge
- Math
- BFS
- ArticulationPoint
- LCA
- SlidingWindow
- LIS
- BinarySearch
- Flow
- Today
- Total
정리충의 정리노트
[백준] 3830: 교수님은 기다리지 않는다 본문
0. 문제 주소
https://www.acmicpc.net/problem/3830
3830번: 교수님은 기다리지 않는다
문제 상근이는 매일 아침 실험실로 출근해서 샘플의 무게를 재는 일을 하고 있다. 상근이는 두 샘플을 고른 뒤, 저울을 이용해서 무게의 차이를 잰다. 교수님의 마음에 들기 위해서 매일 아침부터 무게를 재고 있지만, 가끔 교수님이 실험실에 들어와서 상근이에게 어떤 두 샘플의 무게의 차이를 물어보기도 한다. 이때, 상근이는 지금까지 잰 결과를 바탕으로 대답을 할 수도 있고, 못 할 수도 있다. 상근이는 결과를 출근한 첫 날부터 공책에 적어 두었다. 하지만, 엄
www.acmicpc.net
1. 풀이
처음엔 LCA를 생각했었는데, 트리 구조가 안나와서 다른 방법을 생각해보았다.
[PS/Union-Find] - [BOJ] 2463: 비용에서 parent 배열의 루트 노드에 집합 내 속한 원소들의 개수를 저장하는 방법과 유사하게,
dist 배열을 따로 만들어 루트 노드까지의 거리를 저장해주면 된다.
각 샘플들의 절대 무게는 필요하지 않다. 상대적인 무게만 필요하므로, dist[a] = 3이라면
a 노드는 a의 루트 노드보다 3만큼 무겁다는 것을 뜻하게 저장한다.
기존 union-find에서의 find 함수는 다음과 같다.
int find(int node){
if (p[node] == -1) return node;
return p[node] = find(p[node]);
}
return 구문에서, 재귀적으로 parent 배열에 저장되어 있던 "원래 알고 있던 루트 노드"의 루트 노드를
이번 노드의 루트로 갱신시켜준다.
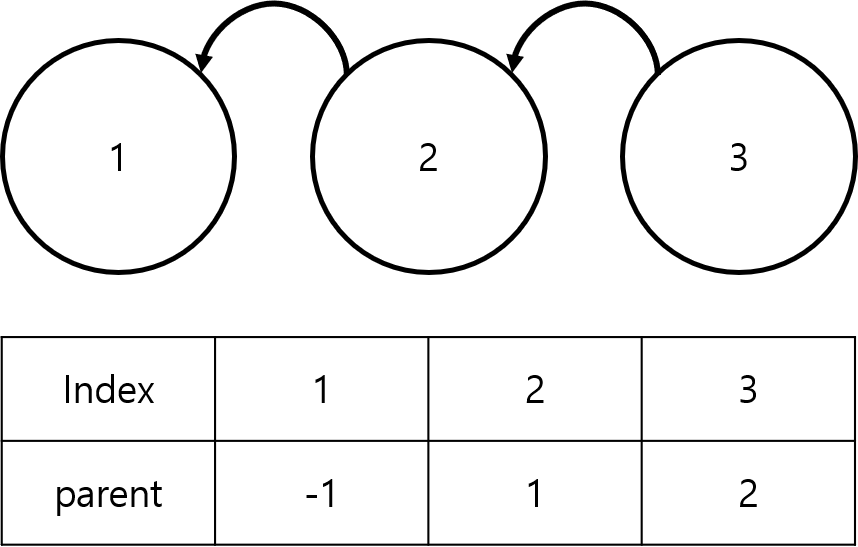
이렇게 되어 있던 상황에서,

이렇게 만들어 주겠다는 뜻이다.
이 기법을 이용해서 dist 배열도 갱신시켜줄 수 있다.
int find(int node){
if (p[node] == -1) return node;
int parent = find(p[node]);
dist[node] += dist[p[node]];
return p[node] = parent;
}
기존과 달라진 점은, 재귀적으로 "find(p[node])를 호출" ~ "p[node]에 이를 저장" 단계 사이에,
dist[node]에 p[node]의 dist를 더해주는 작업을 끼워넣은 것이다.
초기 배열들이 아래와 같이 저장되어있는 예시를 보자.
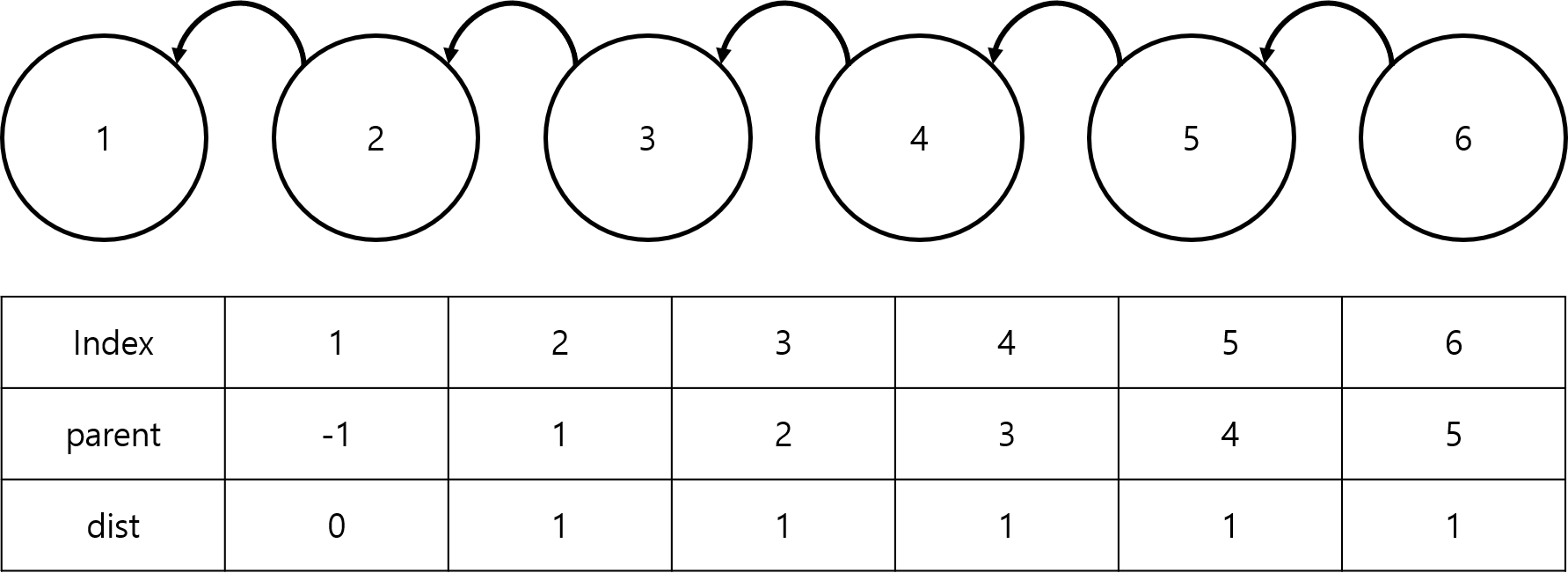
편의상 인접한 번호의 거리는 모두 1로 설정했다.
여기서 기존의 find 함수를 이용하여 2번 ~ 6번 노드의 parent를 모두 1로 설정할 수 있다.
이 때 dist 배열을 함께 갱신해주려 한다. 현재 루트 노드로 알고 있던 노드를 p[node]라고 하자.
그럼 dist[node]는
"node부터 p[node]까지의 거리" + "p[node]부터 루트 노드까지의 거리" 로 갱신되어야 한다.
이것이 dist[node] = dist[node] + dist[ p[node] ] 가 되는 것이다.
6번 노드를 살펴보자. 우리는 6번 노드의 루트 노드를 1번으로 맞춰주려 한다.
현재는 p[6] = 5로 저장되어있다. 위에 적은 식대로라면, dist[node] = 1이고, dist[ p[node] ] = 4가 되어야 한다.
하지만 현재 상황으로는 dist[ p[node] ] = dist[ 5 ] = 1이다. 왜일까?
5번 노드가 현재 루트 노드로 알고 있는 노드는 4번 노드이기 때문이다.
dist[ 6 ]에 dist[ 5 ]를 더해주기 앞서, dist[ 5 ]의 값을 미리 갱신해주어야 한다는 소리다.
int parent = find(p[node]);
dist[node] += dist[p[node]];
return p[node] = parent;
그래서 먼저 find 함수에 재귀적으로 p[node]를 넣어주고, dist[ p[node] ]의 값을 제대로 만든 다음,
dist[node]에 dist[ p[node] ]을 더해주어야 하는 것이다.
이제 merge 함수를 보자.
void merge(int a, int b, int w){
int roota = find(a);
int rootb = find(b);
if (roota == rootb) return;
dist[rootb] = dist[a] - dist[b] + w;
p[rootb] = roota;
return;
}
a, b, w는 각각 문제에서 주어진 그대로, b가 a보다 w만큼 더 크다는 뜻이다.
이를 아래와 같이 나타낼 것이다.
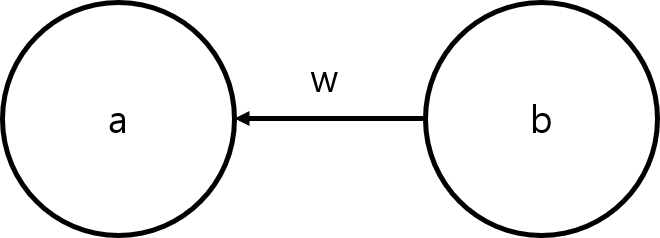
그럼 a와 b가 각각 다른 집합에 있을 때, 조절해주어야 하는 것은 무엇일까?

a 와 b가 다른 집합에 있을 때, ! a b w 라는 명령어가 주어졌다고 해보자.
두 집합을 merge한 뒤의 최종 루트 노드를 roota로 만들려 한다.
루트 노드의 dist는 기본적으로 0으로 설정되어 있다. 우리는 rootb가 roota보다 얼마나 무거운지,
즉 dist[rootb]만 새로 설정해 주면 된다.
rootb가 속한 집합의 노드들은 이 이후에도 아직 자신의 루트가 rootb라고 생각할 것이다.
즉 rootb가 속했던 집합의 노드를 B라고 하면, p[B] = rootb라고 저장이 되어있을 거라는 것이다.
하지만 find(B)를 호출하게 되면, 우리가 find 함수를 재귀적으로 설계한 덕분에, dist[B]가 B부터 roota까지의 거리로
알맞게 조정될 것이다.
그래서 dist[rootb]만 새로 설정해 주면 되는 것이다.
dist[rootb]는 아래 그림을 보면 어떻게 설정해야 할 지 쉽게 감이 잡힌다.
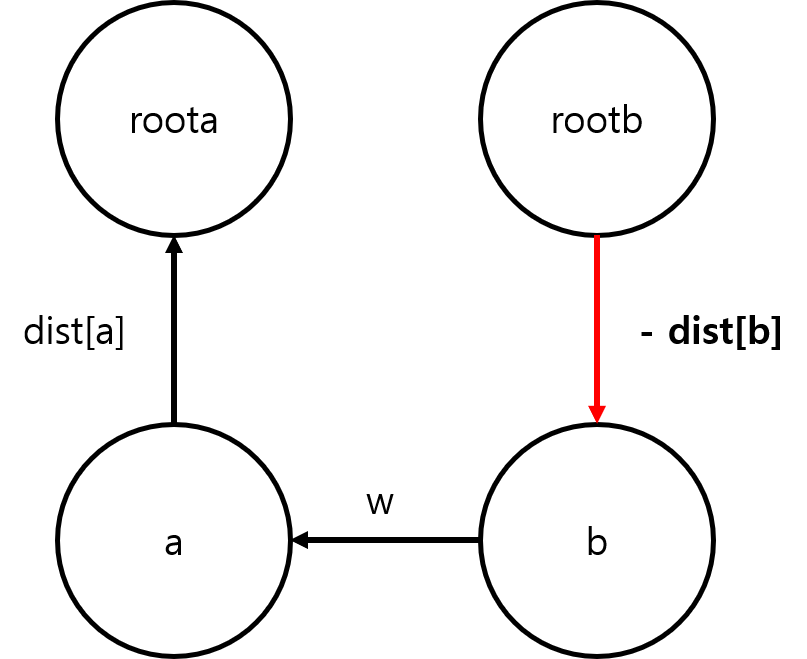
2. 풀이 코드
* 유의할 점
#include <iostream>
#include <cstring>
#define MAX 100005
#define ll long long
using namespace std;
int N, M;
int p[MAX];
ll dist[MAX];
int find(int node){
if (p[node] == -1) return node;
int parent = find(p[node]);
dist[node] += dist[p[node]];
return p[node] = parent;
}
void merge(int a, int b, int w){
int roota = find(a);
int rootb = find(b);
if (roota == rootb) return;
dist[rootb] = dist[a] - dist[b] + w;
p[rootb] = roota;
return;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif // ONLINE_JUDGE
ios_base::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
while(1){
memset(p, -1, sizeof(p));
memset(dist, 0, sizeof(dist));
cin >> N >> M;
if (N == 0 & M == 0) break;
char op;
int a, b, w;
for (int i=0;i<M;i++){
cin >> op;
if (op == '!'){
cin >> a >> b >> w;
merge(a, b, w);
}
else{
cin >> a >> b;
if (find(a) != find(b)){
cout << "UNKNOWN\n";
}
else{
cout << dist[b] - dist[a] << "\n";
}
}
}
}
return 0;
}
'PS > Union-Find' 카테고리의 다른 글
| [백준] 9938: 방 청소 (0) | 2020.04.20 |
|---|---|
| [백준] 2463: 비용 (0) | 2020.02.20 |
