| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- IndexedTree
- Tree
- Sweeping
- BFS
- DP
- topologicalsort
- ShortestPath
- BinarySearch
- backtracking
- Bellman-Ford
- SlidingWindow
- Union-Find
- scc
- Implementation
- 2-sat
- DFS
- LIS
- Floyd
- Flow
- mergesorttree
- ArticulationPoint
- FenwickTree
- LCA
- TwoPointers
- MST
- Math
- greedy
- KMP
- Dijkstra
- Bridge
- Today
- Total
정리충의 정리노트
[백준] 2243: 사탕상자 본문
0. 문제 주소
https://www.acmicpc.net/problem/2243
2243번: 사탕상자
첫째 줄에 수정이가 사탕상자에 손을 댄 횟수 n(1≤n≤100,000)이 주어진다. 다음 n개의 줄에는 두 정수 A, B, 혹은 세 정수 A, B, C가 주어진다. A가 1인 경우는 사탕상자에서 사탕을 꺼내는 경우이다. 이때에는 한 정수만 주어지며, B는 꺼낼 사탕의 순위를 의미한다. 이 경우 사탕상자에서 한 개의 사탕이 꺼내지게 된다. 또, A가 2인 경우는 사탕을 넣는 경우이다. 이때에는 두 정수가 주어지는데, B는 넣을 사탕의 맛을 나타내는 정수이고
www.acmicpc.net
1. 풀이
세그트리를 이용해서 맛의 좋고 나쁨을 나타내는 1부터 100만까지의 수에 대해서, 구간 합을 저장하는 세그트리를 만든다.
맨 처음 사탕의 개수는 모두 0이므로 초기 construct 함수도 필요 없고, 답을 찾는 find 함수 특성상 get_sum 함수도 필요 없다.
필요한 함수는 기존과 동일한 update 함수와, 아래와 같은 find 함수이다.
int find(int node, int s, int e, int remain){
if (s==e) return s;
int mid = (s+e)/2;
int left_child = tree[node*2];
if (remain > left_child){
return find(node*2+1, mid+1, e, remain - left_child);
}
else{
return find(node*2, s, mid, remain);
}
}
"특정 순서에 있는 원소"를 찾는다는 점에서 [PS/DP] - [BOJ] 1256: 사전과 비슷하다.
루트 노드(1번)부터 탐색을 시작해서, remain 값과 왼쪽 자식에 저장되어 있는 값을 비교한다.
remain 값은 남아있는 순서의 개수라고 생각하면 된다.
맨 처음 find 함수를 호출할 땐 구해고자 하는 순위를 넣어주는데, 아래 예시를 보자.
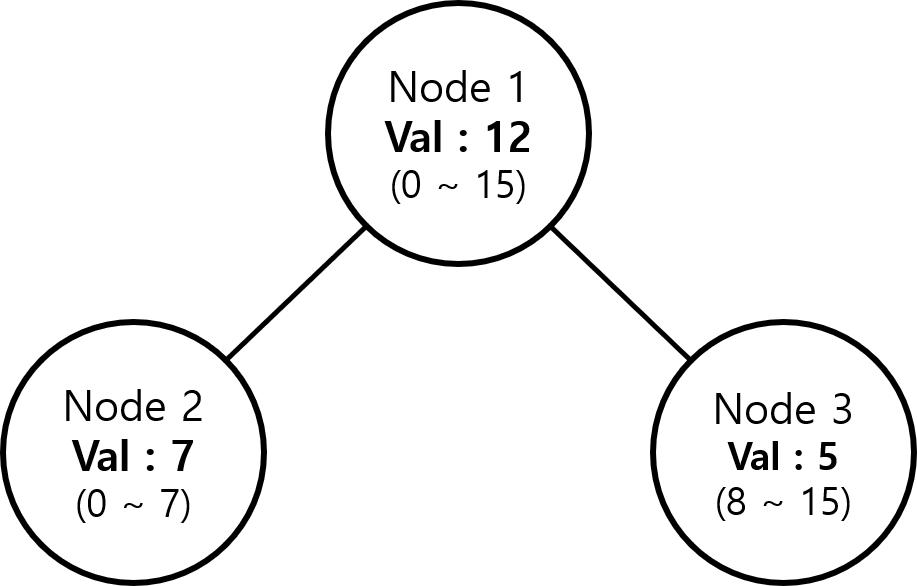
1번 노드에 0번 원소부터 15번 원소까지의 합인 12가 저장되어있고, 그 왼쪽 자식에 7, 오른쪽 자식에 5가 저장되어 있다.
찾고 싶은 순위를 8이라고 해보자.
찾으려하는 값이 왼쪽 자식에 저장되어 있는 7보다 크다.
이는 0번 원소에서 7번 원소 중에는 우리가 원하는 답이 없다는 뜻과 같다.
이 경우 재귀적으로 노드 번호엔 오른쪽 자식의 노드 번호를, remain 값에는 (기존 remain값 - 왼쪽 자식의 값)을 대입해주어
결론적으로 탐색하는 범위의 처음과 끝이 같아질 때 까지 ( s = e ) 탐색을 반복한다.
2. 풀이 코드
* 유의할 점
#include <iostream>
#include <cmath>
#define MAX 1000000
using namespace std;
int N;
int tree[1<<21];
int leaf_size;
void update(int i, int diff){
i += leaf_size;
tree[i] += diff;
while(i>1){
i/=2;
tree[i] = tree[i*2] + tree[i*2+1];
}
}
int find(int node, int s, int e, int remain){
if (s==e) return s;
int mid = (s+e)/2;
int left_child = tree[node*2];
if (remain > left_child){
return find(node*2+1, mid+1, e, remain - left_child);
}
else{
return find(node*2, s, mid, remain);
}
}
int main(){
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif
leaf_size = 1 << (int)(ceil(log2(MAX)));
scanf("%d", &N);
int op, b, c, pos;
for (int i=0;i<N;i++){
scanf("%d", &op);
if (op == 1){
scanf("%d", &b);
pos = find(1, 0, leaf_size-1, b);
printf("%d\n", pos+1);
update(pos, -1);
}
else {
scanf("%d %d", &b, &c);
update(b-1, c);
}
}
return 0;
}
'PS > IndexedTree' 카테고리의 다른 글
| [백준] 7469: K번째 수 (0) | 2020.08.11 |
|---|---|
| [백준] 9342: 디지털 비디오 디스크(DVDs) (0) | 2020.08.11 |
| [백준] 3392: 화성지도 (0) | 2020.07.18 |
| [백준] 10167: 금광 (0) | 2020.04.22 |
| [백준] 2517: 달리기 (0) | 2020.02.18 |

